Автоматный механизм построения тестового сценария

Ориентированным графом будем называть тройку G = ( VG, XG, EG ), в которой:

VG - множество вершин графа;
XG - множество стимулов графа;
EG
VG x XG x VG - множество дуг графа, каждая из которых состоит из начальной вершины, стимула и конечной вершины.

Ориентированный граф G = ( VG, XG, EG )называется конечным, если множества VG, XG, и EG являются конечными.

Стимул s

XG называется допустимым в вершине u

VG ориентированного графа G = ( VG, XG, EG ), если существует дуга ( v, x, v' )

EG, такая что v = u и x = s.

Ориентированный граф G = ( VG, XG, EG ) называется детерминированным, если для каждой вершины u

VG и стимула s

XG существует не более одной дуги ( v, x, v' )

EG, такой что v = u и x = s.

Последовательность дуг ( e1, e2, …, en ) ориентированного графа G = ( VG, XG, EG ) называется маршрутом, если для каждого i = 1, …, n-1 конечная вершина перехода ei совпадает с начальной вершиной перехода ei+1. При этом мы будем говорить, что маршрут ведет из начальной вершины перехода e1 в конечную вершину перехода en.

Бесконечным маршрутом мы будем называть бесконечную последовательность переходов, любой префикс которой является конечным маршрутом.

Ориентированный граф G = ( VG, XG, EG ) называется сильно-связным, если для любых двух его вершин v и v' существует маршрут ( e1, e2, …, en ), ведущий из вершины v в вершину v'.

Обходом конечного ориентированного графа G = ( VG, XG, EG ) называется маршрут v1

…

vn, в котором для каждой дуги ( v, x, v' )

EG существует i

{ 1, … , n-1 }, такое что v = vi, x = xi и v' = vi+1.

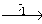
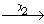
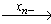
Определение 6.

Алгоритмом движения на ориентированных графах называется функция α, которая по ориентированному графу G = ( VG, XG, EG ), текущей вершине v

VG и пройденному маршруту ( e1, e2, …, en ) определяет следующее действие a

{ τ }. Следующее действие может быть либо стимулом x, допустимым в текущей вершине, либо специальным значением τ, символизирующим пустое действие.

Ориентированным графом будем называть тройку G = ( VG, XG, EG ), в которой:

VG - множество вершин графа;
XG - множество стимулов графа;
EG
VG x XG x VG - множество дуг графа, каждая из которых состоит из начальной вершины, стимула и конечной вершины.

Ориентированный граф G = ( VG, XG, EG )называется конечным, если множества VG, XG, и EG являются конечными.

Стимул s

XG называется допустимым в вершине u

VG ориентированного графа G = ( VG, XG, EG ), если существует дуга ( v, x, v' )

EG, такая что v = u и x = s.

Ориентированный граф G = ( VG, XG, EG ) называется детерминированным, если для каждой вершины u

VG и стимула s

XG существует не более одной дуги ( v, x, v' )

EG, такой что v = u и x = s.

Обходом конечного ориентированного графа G = ( VG, XG, EG ) называется маршрут v1

…

vn, в котором для каждой дуги ( v, x, v' )

EG существует i

{ 1, … , n-1 }, такое что v = vi, x = xi и v' = vi+1.

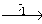
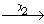
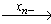
Определение 6.

VG и пройденному маршруту ( e1, e2, …, en ) определяет следующее действие a

Функционированием алгоритма движения α на ориентированном графе G = ( VG, XG, EG ) с начальной вершины v0

V называется конечный или бесконечный маршрут ( e1, e2, …, en, … ) в графе G, удовлетворяющий следующим условиям:

начальная вершина v1 первой дуги маршрута e1 = ( v1, x1, v'1 ) совпадает с начальной вершиной v0;
в каждой дуге маршрута ei = ( vi, xi, v'i ) стимул xi равен α( A, vi, ( e1, …, ei-1 ) ) - значению алгоритма движения α на автомате A, начальной вершине vi и пройденном маршруте ( e1, …, ei-1 );
если дуга ei = ( vi, xi, v'i ) является последней в последовательности, то α( A, v'i, ( e1, …, ei ) ) = τ.

Алгоритм движения α называется алгоритмом обхода на классе конечных ориентированных графов Æ, если на любом графе G из класса Æ любое функционирование алгоритма движения α является конечным обходом графа G.

Алгоритм движения α называется неизбыточным, если для любых двух конечных ориентированных графов G1 = ( VG1, XG1, EG1 ) и G2 = ( VG2, XG2, EG2 ), для любой вершины v

VG1 ∩ VG2 и для любого пройденного маршрута ( e1, …, en ), из равенства множеств допустимых стимулов в текущей вершине и в каждой вершине из пройденного маршрута следует равенство α( A1, v, ( e1, …, en ) ) = α( A2, v, ( e1, …, en ) ). Другими словами, алгоритм движения является неизбыточным, если он зависит только от текущей вершины, пройденного маршрута и множества допустимых стимулов в текущей вершине и в каждой вершине из пройденного маршрута.

Преимущество неизбыточных алгоритмов заключается в том, что для начала их работы не требуется полное описание ориентированного графа. Вся информация о вершинах и дугах графа, используемая неизбыточным алгоритмом, может быть извлечена в процессе движения по графу.

В работах [, , ] представлено исследование неизбыточных алгоритмов обхода различных классов графов. В частности, в [] рассмотрен неизбыточный алгоритм обхода αdfsm на классе детерминированных сильно-связных конечных ориентированных графах.

Этот алгоритм используется в технологии UniTesK в качестве основного алгоритма для построения последовательностей тестовых воздействий.

Неизбыточным описанием ориентированного графа называется тройка ( VG, XG, π ), где

VG - множество вершин графа,
XG - множество стимулов графа,
π : VG

(XG) - функция, определяющая множество допустимых стимулов в данной вершине графа.

Неизбыточное описание ориентированного графа содержит все необходимое для работы неизбыточного алгоритма движения. С другой стороны, для разработчика теста значительно проще создать такое описание, чем описывать граф в явном виде. Поэтому в технологии UniTesK неизбыточное описание графа нашло свое применение при определении тестовых сценариев.

Автоматным тестовым сценарием для целевой системы с интерфейсом ( X, Y, V ) называется семерка ( IG, vg0, α, S, ρ, γ, η ), где

IG = ( VG, XG, π ) - неизбыточное описание ориентированного графа, называемого графом сценария,
vg0 : V
VG - функция инициализации графа сценария,
α - неизбыточный алгоритм движения по графу сценария,
S - множество состояний сценария,
ρ : S
S - функция рестарта сценария,
γ : VG x XG

( X, Y, V, S ) - отображение, ставящее в соответствие каждым вершине графа сценария и стимулу, допустимому в этой вершине, тестовый сценарий, который мы будем называть сценарным воздействием,
η : VG x XG x V x S
VG - отображение, ставящее в соответствие конечную вершину дуги графа сценария для данных начальной вершины и стимула графа сценария и состояний сценария и целевой системы после выполнения сценарного воздействия.

Автоматным механизмом построения тестового сценария называется функция, преобразующая автоматный тестовый сценарий ( IG, vg0, α, S, ρ, γ, η ) в тестовый сценарий, посредством вспомогательного определения тестового сценария с внутренними переходами σε = ( ( S', A, B, E, Q ), s0 ) по следующим правилам:

S' = VG x S
{ ε } x V x EG* - состояние тестового сценария состоит из:
- текущей вершины графа сценария vg,
- текущего состояния сценария s, которое может принимать дополнительное значение ε, которое означает неинициализированное состояние,
- текущего состояния целевой системы v,
- пройденного маршрута в графе сценария path. Здесь множество EG* обозначает множество всех конечных списков элементов из множества дуг EG = VG x XG x VG.
множество стимулов A = X
V
{ ε }, согласно определению тестового сценария с внутренними переходами;
множество реакций B = (Y x V)
{ ε }, согласно определению тестового сценария с внутренними переходами;
E = { ( ( vg, s, v, path ), a, b, ( vg', s', v', path' ) )
S' x A x B x S' | (α( IG, vg, path ) ≠ τ)

(v' = state( a, b, v ))

(s
γQ( vg, xg )
(vg' = vg)
(path' = path)
( s, a, b, s' )
γE( vg, xg ))

(s
γQ( vg, xg )
(vg' = η( vg, xg, v, s ))
(path' = path ^ ( vg, xg, vg' ))

(a = ε)
(b = ε)
(s' = ρ( s ))
)
}, где использовались следующие сокращения
xg ≡ α( IG, vg, path );
state( a, b, v ) = a, если a
V;
state( a, b, v ) = vb, если b = ( yb, vb )
Y x V;
state( a, b, v ) = v, иначе;
Q = { ( vg, s, v0, path )
S' | α( IG, vg, path ) = τ } - заключительными состояния сценария являются состояния, в которых алгоритм движения возвращает пустое действие τ;
s0(v0) = ( vg0(v0), γS0( vg, α( IG, vg0(v0),

) )(v0), v0,

), если α( IG, vg0(v0),

) ≠ τ,
s0(v0) = ( vg0(v0), ε, v0,

), если α( IG, vs0(v0),

) = τ,

- инициализирующая функция, которая устанавливает следующие начальные значения:
текущая вершина графа сценария определяется при помощи функции инициализации графа сценария;
текущее состояние сценария s принимает
значение, вычисленное посредством инициализирующей функции первого сценарного воздействия, если таковое найдено при помощи алгоритм движения α,
неинициализированное значение, в противном случае;
текущее состояние целевой системы инициализируется параметром функции,
пройденный маршрут инициализируется пустым списком.

Далее для построения тестового сценария автоматный механизм использует определенное ранее преобразование тестового сценария с внутренними переходами в тестовый сценарий без внутренних переходов.

Работа автоматного механизма построения тестового сценария устроена следующим образом. Граф сценария описывает некоторым образом пространство тестовых ситуаций. Автоматный механизм двигается по данному графу, используя заданный алгоритм движения.

Алгоритм движения выбирает стимул, который необходимо подать в текущей вершине. Автоматный механизм определяет тестовый сценарий, который приписан паре вершина-стимул графа сценария, и выполняет его. По результатам выполнения механизм вычисляет новую вершину графа сценария и повторяет этот цикл до тех пор, пока алгоритм движения не завершит свою работу.

Все тестовые сценарии, приписанные к графу сценария, разделяют общее состояние, которое позволяет им накапливать информацию о процессе тестирования. После завершения каждого сценария автоматный механизм обновляет это состояние при помощи функции рестарта сценария. Благодаря этому, один и тот же тестовый сценарий может успешно применяться несколько раз подряд.

Пара отображений γ и η определяет дуги графа сценария, основываясь на поведении целевой системы. Таким образом, граф сценария строится динамически посредством применения этих отображений. В него входят те дуги, которые были "пройдены" в процессе тестирования.

Функционированием алгоритма движения α на ориентированном графе G = ( VG, XG, EG ) с начальной вершины v0

V называется конечный или бесконечный маршрут ( e1, e2, …, en, … ) в графе G, удовлетворяющий следующим условиям:

начальная вершина v1 первой дуги маршрута e1 = ( v1, x1, v'1 ) совпадает с начальной вершиной v0;
в каждой дуге маршрута ei = ( vi, xi, v'i ) стимул xi равен α( A, vi, ( e1, …, ei-1 ) ) - значению алгоритма движения α на автомате A, начальной вершине vi и пройденном маршруте ( e1, …, ei-1 );
если дуга ei = ( vi, xi, v'i ) является последней в последовательности, то α( A, v'i, ( e1, …, ei ) ) = τ.

VG - множество вершин графа,
XG - множество стимулов графа,
π : VG

(XG) - функция, определяющая множество допустимых стимулов в данной вершине графа.

IG = ( VG, XG, π ) - неизбыточное описание ориентированного графа, называемого графом сценария,
vg0 : V
VG - функция инициализации графа сценария,
α - неизбыточный алгоритм движения по графу сценария,
S - множество состояний сценария,
ρ : S
S - функция рестарта сценария,
γ : VG x XG

( X, Y, V, S ) - отображение, ставящее в соответствие каждым вершине графа сценария и стимулу, допустимому в этой вершине, тестовый сценарий, который мы будем называть сценарным воздействием,
η : VG x XG x V x S
VG - отображение, ставящее в соответствие конечную вершину дуги графа сценария для данных начальной вершины и стимула графа сценария и состояний сценария и целевой системы после выполнения сценарного воздействия.

S' = VG x S
{ ε } x V x EG* - состояние тестового сценария состоит из:
- текущей вершины графа сценария vg,
- текущего состояния сценария s, которое может принимать дополнительное значение ε, которое означает неинициализированное состояние,
- текущего состояния целевой системы v,
- пройденного маршрута в графе сценария path. Здесь множество EG* обозначает множество всех конечных списков элементов из множества дуг EG = VG x XG x VG.
множество стимулов A = X
V
{ ε }, согласно определению тестового сценария с внутренними переходами;
множество реакций B = (Y x V)
{ ε }, согласно определению тестового сценария с внутренними переходами;
E = { ( ( vg, s, v, path ), a, b, ( vg', s', v', path' ) )
S' x A x B x S' | (α( IG, vg, path ) ≠ τ)

(v' = state( a, b, v ))

(s
γQ( vg, xg )
(vg' = vg)
(path' = path)
( s, a, b, s' )
γE( vg, xg ))

(s
γQ( vg, xg )
(vg' = η( vg, xg, v, s ))
(path' = path ^ ( vg, xg, vg' ))

(a = ε)
(b = ε)
(s' = ρ( s ))
)
}, где использовались следующие сокращения
xg ≡ α( IG, vg, path );
state( a, b, v ) = a, если a
V;
state( a, b, v ) = vb, если b = ( yb, vb )
Y x V;
state( a, b, v ) = v, иначе;
Q = { ( vg, s, v0, path )
S' | α( IG, vg, path ) = τ } - заключительными состояния сценария являются состояния, в которых алгоритм движения возвращает пустое действие τ;
s0(v0) = ( vg0(v0), γS0( vg, α( IG, vg0(v0),

) )(v0), v0,

), если α( IG, vg0(v0),

) ≠ τ,
s0(v0) = ( vg0(v0), ε, v0,

), если α( IG, vs0(v0),

) = τ,

- инициализирующая функция, которая устанавливает следующие начальные значения:
текущая вершина графа сценария определяется при помощи функции инициализации графа сценария;
текущее состояние сценария s принимает
значение, вычисленное посредством инициализирующей функции первого сценарного воздействия, если таковое найдено при помощи алгоритм движения α,
неинициализированное значение, в противном случае;
текущее состояние целевой системы инициализируется параметром функции,
пройденный маршрут инициализируется пустым списком.