Сценарные функции

В данном разделе мы рассмотрим метод описания тестовых сценариев, приписанных к дугам графа сценария. В основе метода лежит понятие сценарной функции, которое представляет собой параметризованное семейство тестовых сценариев.

Сценарной функцией для целевой системы с интерфейсом ( X, Y, V ) называется шестерка ( GS, PS, IS, C, is0, π ), где:

• GS - множество внешних состояний;
• PS - множество параметризующих состояний;
• IS - множество внутренних состояний;
• C = ( CS, A, B, E, Q ) - управляющий автомат, в котором:
• CS = GS x PS x IS - состояние автомата состоит из декартова произведения всех видов состояний сценарной функции,
• A = X
  
  V,
• B = (Y x V)
  
  { ε },
• E
  
  CS x A x B x CS,
• Q
  
  CS;
• is0 : V x GS
  
  IS - функция инициализации сценарной функции;
• π : V x GS
  
  
  (PS) - функция, определяющая множество параметризующих состояний для данных внешнего состояния и состояния целевой системы. Это множество мы будем называть множеством параметров.

Множество всех сценарных функций для целевой системы с интерфейсом ( X, Y, V ) и имеющее множество внешних состояний GS мы будем обозначать Σ( X, Y, V, GS ).

Автоматным тестовым сценарием со сценарными функциями для целевой системы с интерфейсом ( X, Y, V ) называется шестерка ( GS, gs0, VG, vg, α,

), где:

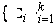
• GS - множество глобальных состояний сценария;
• gs0 : V
  
  GS - функция инициализации глобального состояния;
• VG - множество вершин графа автомата;
• vg : V x GS
  
  VG - функция вычисления вершины графа сценария;
• α - неизбыточный алгоритм движения по графу сценария,
• 
  - конечный набор сценарных функций Σi
  
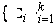  Σ( X, Y, V, GS ).

Множества параметров всех сценарных функций должны быть согласованы с вершинами графа сценария:

i { 1, …, k } v1,v2 V gs1,gs2 GS

vg( v1, gs1 ) = vg( v2, gs2 )

πΣi( v1, gs1 ) = πΣi( v2, gs2 ).

Другими словами, для любой пары значений состояния целевой системы и глобального состояния сценария, отображающейся в одну вершину графа сценария, множества параметров всех сценарных функций должны совпадать.

Исходя из этого ограничения, можно определить множество параметров сценарной функции Σi в данной вершине графа vg как:

• πΣi( v, gs ), если
  
  v
  
  V
  
  gs
  
  GS : vg( v, gs ) = vg;
• {}, иначе.

В автоматном тестовом сценарии со сценарными функциями набор сценарных функций используется не только для описания тестовых сценариев приписанных к дугам графа, но и для описания множества стимулов графа. Далее, мы определим семантику автоматных тестовых сценариев со сценарными функциями посредством описания механизма преобразования таких сценариев в тестовый сценарий.

Автоматным механизмом сценарных функций называется функция, преобразующая автоматный тестовый сценарий со сценарными функциями ( GS, gs0, VG, vg, α, ) в тестовый сценарий, посредством применения автоматного механизма построения тестового сценария к автоматному тестовому сценарию ( IG', vg0', α', S', ρ', γ', η' ), определенному по следующим правилам:

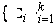
• неизбыточное описание ориентированного графа IG' = ( VG', XG', π' ) состоит из:
  
  
  
  • множества вершин, совпадающего с множеством вершин графа автомата VG (VG' = VG),
  • множества стимулов, являющегося дизъюнктивным объединением параметризующих состояний всех сценарных функций (XG' =
    
    ),
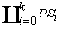
  • функции, определяющей множество допустимых стимулов π' =
    
    ;
  
  
  
• функция инициализации графа сценария vg0': vg0'(v) ≡ vg( v, gs0(v) );
• неизбыточный алгоритм α' = α;
• множество состояний сценария S' = GS x V x State,
  где State =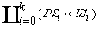
  
  
  {ε};
• функция рестарта сценария ρ': ρ'( (gs,v,state) ) ≡ ( gs, v, ε );
• сценарное воздействие γ'( vg, psi ) = ( ( S', A', B', E', Q' ), s'0 )
  
  
  ( X, Y, V, S' ) определяется для каждой пары ( vg, psi ) следующим образом:
  
  
  
  • A' = X
    
    V,
  • B' = (Y x V)
    
    { ε },
  • E' = { ( ( gs, v, state ), a, b, ( gs', ( ps'i, v', is'i) ) ) :
    
    ( ( state = ε )
    
    
    
    ( ( gs, psi, isi,0( v, gs ) ), a, b, ( gs', ps'i, is'i ) )
    
    Ei
    
    
    )
    
    
    
    ( (
    
    isi
    
    ISi state = ( psi, isi) )
    
    
    
    ( ( gs, psi, isi ), a, b, ( gs', ps'i, is'i ) )
    
    Ei
    )
    
    
    
    ( a
    
    V )
    
    v' = a
    
    
    
    ( b = ( yb, vb )
    
    Y x V )
    
    v' = vb },
    
    
  • Q' = { ( gs, v, state )
    
    S' :
    ( ( state = ε )
    
    
    ( gs, psi, isi,0( v, gs ) )
    
    Qi
    )
    
    
    
    ( (
    
    isi
    
    ISi state = ( psi, isi) )
    
    ( gs, psi, isi )
    
    Qi
    )
    },
  • s'0(v0) = ( gs0(v0), v0, ε );
  
  
  
• отображение η'( vg1, psi, v, ( gs, v2, state ) ) = vg( v, gs ).

Таким образом, автоматный тестовый сценарий со сценарными функциями определяет тестовый сценарий, являющийся последовательной композицией тестовых сценариев приписанных к дугам графа сценария. Правила выбора последовательности дуг графа определяются алгоритмом движения, который учитывает при этом поведение целевой системы.


Содержание раздела

---

---