Стационарный автоматный тестовый сценарий
Рассмотрим реализацию предложенного подхода более формально.
Стационарным автоматным тестовым сценарием относительно асинхронной модели требований A = ( V, X, Y, Z, E ) с множеством стабильных состояний VS


- SA = ( DA, Afsm, VG, XG, vg0, α, ) - асинхронный автоматный тестовый сценарий со сценарными функциями для целевой системы с асинхронным интерфейсом ( X, Y, Z ),
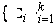
- ASt = ( SSt, s0,St, XSt, YSt, ESt, QSt ) - выделенный взаимодействующий автомат, входящий в состав DA, и называемый стабилизирующим автоматом асинхронного тестового сценария DA,
- AIR Ã( Unit,
 ( Ω(X,Y,Z) ) ) - асинхронная функция, замыкание которой по множеству { stop, abort } входит в состав DA,
( Ω(X,Y,Z) ) ) - асинхронная функция, замыкание которой по множеству { stop, abort } входит в состав DA,
- AHO Ã(
 ( Ω(X,Y,Z) ) x V, Bool x V ) - асинхронная функция, замыкание которой по множеству { stop, abort } входит в состав DA,
( Ω(X,Y,Z) ) x V, Bool x V ) - асинхронная функция, замыкание которой по множеству { stop, abort } входит в состав DA,
- AGS Ã( Unit, VG ) - асинхронная функция, замыкание которой по множеству { stop, abort } входит в состав DA;

и для которой выполнены следующие ограничения:
- вхождения замыканий взаимодействующих автоматов AIR, AHO и AGS и вхождения ASt, Afsm и Σi в DA различаются между собой,
- SSt = ( { s0, s1, s2, s4, s5, s6, final } Ω(X,Y,Z) ) x V,

- s0,St = ( s0, v0 ),
- XSt = { callIR, callGS, abort } { callHO,P,v | P
 Ω(X,Y,Z), v
Ω(X,Y,Z), v V },
V },
- YSt =
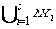 { stop, abort }
{ stop, abort } { resultHO,verdict,v | verdict
{ resultHO,verdict,v | verdict Bool, v
Bool, v V }
V }
{ resultIR,P | P Ω(X,Y,Z) },
Ω(X,Y,Z) },
где RXi = { resulti,true, resulti,false },
- ESt = { ( ( s0, v ) resulti,true?, ( s1, v ) ) | i = 1, …, k }
{ ( ( s1, v ), callIR!, ( s2, v ) ) }
{ ( ( s2, v ), resultIR,P?, ( P, v ) ) | P Ω(X,Y,Z) }
Ω(X,Y,Z) }
Основную роль здесь играет стабилизирующий автомат, который после завершения каждого цикла работы сценарной функции запрашивает модель поведения, описывающую все взаимодействия с целевой системой за время этого цикла, и проверяет корректность этой модели поведения. В случае успешной проверки стабилизирующий автомат возвращает управление управляющему автомату с указанием новой вершины в графе автомата. В противном случае тест завершается посылкой стимула abort.
Работа по оценке корректности модели поведения выполняется в асинхронной функции AHO, которая получает на вход текущее состояние модели требований и асинхронную модель поведения. К модели поведения применяется стабилизирующая трансформация и затем проверяется корректность этой трансформации относительно стабилизирующей трансформации модели требований ST[A,VS] с начальным состоянием, равным текущему состоянию модели требований. В дополнение к оценке корректности AHO возвращает основную составляющую конечного состояния линеаризации, которая становится новым текущим состоянием модели требований.
Однако, конечное состояние линеаризации может быть найдено только в том случае, когда все успешные линеаризации модели поведения ST[P] завершаются в одном и том же состоянии. Если это условие не выполняется, то асинхронная функция AHO не может выполнить свою задачу и, соответственно, стационарный автоматный тестовый сценарий не может быть применен.
Далее, мы обратимся к вопросу применимости стационарного автоматного тестового сценария и определим достаточные условия для его корректной работы.
Асинхронная модель требований A = ( V, X, Y, Z, E ) называется стационарно-детерминированной относительно множества стабильных состояний VSV, если для любого конечного мультимножества асинхронных взаимодействий P и для любого состояния v VS
VS
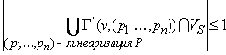
Лемма.
Если асинхронная модель требований A = ( V, X, Y, Z, E ) является стационарно-детерминированной относительно множества стабильных состояний VSV, то произвольный стационарный автоматный тестовый сценарий относительно модели требований A с множеством стабильных состояний VS и начальным состоянием v0 VS применим независимо от поведения целевой системы.
VS применим независимо от поведения целевой системы.
То есть v'VS, что и требовалось доказать.
2. В качестве завершающего шага мы докажем, что для любой асинхронной модели поведения P, если стабилизирующая трансформация этой модели ST[P] удовлетворяет стабилизирующей трансформации ST[A,VS] с начальным состоянием (v,T), где v стабильно (vVS), то конечное состояние линеаризации (v',x') существует. Из этого следует, что асинхронная функция AHO всегда может выполнить свою задачу, так как согласно первому пункту она всегда получает на вход только стабильные состояния модели требований.
Предположим, что это не так. То есть существует асинхронная модель поведения P, стабильное состояние модели требований vVS и два состояния (v',x') и (v'',x'') такие, что
{ (v',x'), (v'',x'') } и (v',x') ≠ (v'',x'').
и (v',x') ≠ (v'',x'').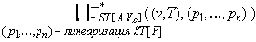
Тогда существует две линеаризации модели поведения ST[P] ( p1,1, p1,2, …, p1,n ) и ( p2,1, p2,2, …, p2,n ) такие, что
(v', x') ( (v,T), ( p1,1, p1,2, …, p1,n ) ) и
( (v,T), ( p1,1, p1,2, …, p1,n ) ) и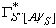
(v'',x'') ( (v,T), ( p2,1, p2,2, …, p2,n ) ).
( (v,T), ( p2,1, p2,2, …, p2,n ) ).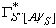
Повторяя рассуждения из первого пункта, можно показать, что x' = x'' = T, p1,n = p2,n = (done,ε), v'VS, v'' VS и
VS и
(v', F) ( (v,T), ( p1,1, p1,2, …, p1,n-1 ) ) и
( (v,T), ( p1,1, p1,2, …, p1,n-1 ) ) и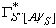
(v'',F) ( (v,T), ( p2,1, p2,2, …, p2,n-1 ) ).
( (v,T), ( p2,1, p2,2, …, p2,n-1 ) ).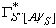
То есть в асинхронной модели требований ST[A,VS] существует путь, начинающийся в (v,T), помеченный ( p1,1, p1,2, …, p1,n-1 ) и заканчивающийся в (v', F):
(v,T)(v2,x2)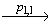 …
…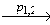 (v', F).
(v', F).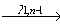
Так как { p1,1, p1,2, …, p1,n-1 }( (X x Y) Z ), то из определения ST[A,VS] следует, что в исходной модели требований A существует путь
Z ), то из определения ST[A,VS] следует, что в исходной модели требований A существует путь
vv2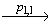 …
…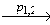 v'.
v'.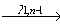
Следовательно, v' ( v, ( p1,1, p1,2, …, p1,n-1 ) ).
( v, ( p1,1, p1,2, …, p1,n-1 ) ).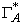
Аналогично, v'' ( v, ( p2,1, p2,2, …, p2,n-1 ) ).
( v, ( p2,1, p2,2, …, p2,n-1 ) ).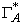
И так как мультимножества взаимодействий { p1,1, p1,2, …, p1,n-1 } и { p2,1, p2,2, …, p2,n-1 } совпадают, то существует мультимножество взаимодействий P* = { p1,1, p1,2, …, p1,n 1 }:
{ v', v'' } , причем v' ≠ v'' и v'
, причем v' ≠ v'' и v'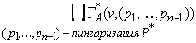 VS, v''
VS, v'' VS.
VS.
То есть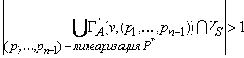
Предположим также, что в процессе работы стационарного автоматного тестового сценария ( SA, ASt, AIR, AHO, AGS ) относительно модели требований A с множеством стабильных состояний VS и начальным состоянием v0VS асинхронная функция AIR последовательно возвращала стабилизирующему автомату асинхронные модели поведения . Тогда, все вердикты функции AHO, посланные стабилизирующему автомату, были положительными, в том, и только в том случае, когда последовательная композиция стабилизирующих трансформаций моделей поведения
. Тогда, все вердикты функции AHO, посланные стабилизирующему автомату, были положительными, в том, и только в том случае, когда последовательная композиция стабилизирующих трансформаций моделей поведения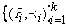 удовлетворяет стабилизирующей трансформации модели требований ST[A] с начальным состоянием v0.
удовлетворяет стабилизирующей трансформации модели требований ST[A] с начальным состоянием v0.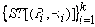
Доказательство.
1. Докажем утверждение леммы в прямую сторону. Предположим, что все вердикты функции AHO, посланные стабилизирующему автомату, были положительными, и покажем, что последовательная композицияудовлетворяет ST[A] с начальным состоянием v0.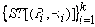
В пункте 2 предыдущей леммы мы показали, что если асинхронная функция AHO получает на вход асинхронную модель поведения Pi и состояние модели требований v и возвращает положительный вердикт и конечное состояние линеаризации v', то в модели требований ST[A] существует путь (v,T)…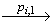 (v',F)
(v',F)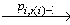 (v',T) для некоторой линеаризации ( pi,1, pi,2, …, pi,n(i)-1, pi,n(i) ) модели ST[Pi] и pi,n (i) = done.
(v',T) для некоторой линеаризации ( pi,1, pi,2, …, pi,n(i)-1, pi,n(i) ) модели ST[Pi] и pi,n (i) = done.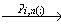
Как мы уже отмечали, функция AHO получает на вход состояние модели требований, которое хранится в стабилизирующем автомате сценария. Это состояние инициализируется в начале работы сценария начальным состоянием v0, а в дальнейшем оно изменяется только в переходах вида ( ( s4, v ), resultHO,true,v'?, ( s5, v' ) ). Эти переходы осуществляются при получении результата от асинхронной функции AHO, так как согласно четырнадцатому ограничению стационарного автоматного тестового сценария каждой реакции получения результата асинхронной функции AHO из стабилизирующего автомата resultHO,true,v' соответствует единственный в рамках DA стимул, принадлежащий соответствующей асинхронной функции.
Отсюда следует, что в модели требований ST[A] существует путь
где ( p1,1, …, p1,n(1)-1, p1,n(1) , p2,1, …, p2,n(2)-1, p2,n(2) , …, pk,1, …, pk,n(k)-1, pk,n(k) ) - некоторая линеаризацией последовательной композиции. Согласно определению стабилизирующей трансформации максимальным элементом в SP[ (Pi,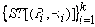 i) ] является псевдовзаимодействие (done,ε). Следовательно
i) ] является псевдовзаимодействие (done,ε). Следовательно i
i {1,…,k} pi,n(i) = (done,ε).
{1,…,k} pi,n(i) = (done,ε).
По определению стабилизирующей трансформации модели требований ST[A] все переходы, помеченные (done,ε), имеют вид ( (w,F), (done,ε), (w,T) ), где wVS. То есть
i {1,…,k} (vi,n(1)-1, xi,n(i)-1)
{1,…,k} (vi,n(1)-1, xi,n(i)-1) (vi,n(i) , xi,n(i) ) ≡ (v'i,F)
(vi,n(i) , xi,n(i) ) ≡ (v'i,F)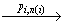 (v'i,T),
(v'i,T),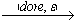
где v'iVS.
Докажем по индукции, чтоi {1, …, k-1} в результате i-го вызова функции AHO из стабилизирующего автомата, та возвращает состояние модели требований равное v'i.
{1, …, k-1} в результате i-го вызова функции AHO из стабилизирующего автомата, та возвращает состояние модели требований равное v'i.
База индукции . Согласно определению стабилизирующего автомата функция AHO в первый раз получает модель поведения (P1,1) и состояние v0 VS. Если k > 1, то функция возвращает положительный вердикт и основную составляющую конечного состояния линеаризации ( v', x' ). Так как модель требований A является стационарно-детерминированной, то конечное состояние линеаризации существует, причем v' = v'1, так как (v0,T)
VS. Если k > 1, то функция возвращает положительный вердикт и основную составляющую конечного состояния линеаризации ( v', x' ). Так как модель требований A является стационарно-детерминированной, то конечное состояние линеаризации существует, причем v' = v'1, так как (v0,T) …
…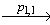 (v'1,F)
(v'1,F)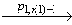 (v'1,T) является успешной линеаризацией модели (P1,
(v'1,T) является успешной линеаризацией модели (P1,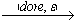 1).
1).
Предположение индукции . Предположим, что после i-го вызова функции AHO из стабилизирующего автомата, та возвращает состояние модели требований v'i.
Шаг индукции . Докажем, что если после i+1-го вызова функция AHO возвращает положительный вердикт и состояние модели требований w, то w = v'i+1.
По определению стабилизирующего автомата при i+1-ом вызове функция AHO получает модель поведения (Pi+1,i+1) и состояние v'i VS. Если i+1 < k, то по условиям леммы функция возвращает положительный вердикт и основную составляющую конечного состояния линеаризации w. Заметим, что в автомате ST[A] существует путь (v'i,T)
VS. Если i+1 < k, то по условиям леммы функция возвращает положительный вердикт и основную составляющую конечного состояния линеаризации w. Заметим, что в автомате ST[A] существует путь (v'i,T) …
…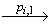 (v'i+1,F)
(v'i+1,F)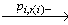 (v'i+1,T), который является одной из успешных линеаризаций модели (Pi+1,
(v'i+1,T), который является одной из успешных линеаризаций модели (Pi+1, i+1).
i+1).
Содержание раздела