Тестовый сценарий

Тестом целевой системы с интерфейсом ( X, Y, V ) называется конечная или бесконечная последовательность взаимодействий { ( vi, xi, yi, v'i ) }. Множество всех тестов целевой системы с интерфейсом ( X, Y, V ) будем обозначать символом ℵ( X, Y, V ).

Моделью поведения целевой системы в ходе теста { ( vi, xi, yi, v'i ) } будем называть мультимножество взаимодействий { ( vi, xi, yi, v'i ) }.

Тест { ( vi, xi, yi, v'i ) } целевой системы с интерфейсом ( X, Y, V ) будем называть успешным относительно модели требований A = ( V, X, Y, E ), если модель поведения в ходе теста удовлетворяет модели требований A. В противном случае, тест будет называться неуспешным.

Определение 4.

Тестовым сценарием для целевой системы с интерфейсом ( X, Y, V ) называется пара ( C, s0 ), где

C - управляющий автомат ( S, A, B, E, Q ), в котором
множество стимулов A = X
V,
множество реакций B = (Y x V)
{ ε },
множество переходов включает в себя только переходы ( s, a, b, s' ), в которых либо a
X и b
(Y x V), либо a
V и b = ε;
s0 : V
S - функция инициализации.

Тестовый сценарий управляет процессом тестирования, выполняя одно из двух возможных действий: либо подавая стимул x

X, либо устанавливая новое состояние v

V. Реакцией на первое действие является реакция целевой системы y и ее постсостояние v', а на второе - пустая реакция ε. Функция инициализации определяет начальное состояние управляющего автомата в зависимости от начального состояния целевой системы.

Множество всех тестовых сценариев для целевой системы с интерфейсом ( X, Y, V ) будем обозначать символом

( X, Y, V ). Множество тестовых сценариев для целевой системы с интерфейсом ( X, Y, V ) и с заданным множеством состояний управляющего автомата S будет обозначаться

( X, Y, V, S ).

Пусть { ej = ( sj, aj, bj, s'j ) } является функционированием тестового сценария σ для целевой системы с интерфейсом ( X, Y, V ).
Тогда { ek(i) = ( sk(i), ak(i), bk(i), s'k(i) ) } будем обозначать подпоследовательность последовательности { ej } составленную из переходов, действия которых связаны с подачей стимула ( ak(i)

X ).

Результатом применения тестового сценария σ = ( C = ( S, A, B, E, Q ), s0 ) к целевой системе, находящейся в начальном состоянии v0

V, является тест { ( vi, xi, yi, v'i ) }, для которого существует такое функционирование управляющего автомата C с начальным состоянием s0(v0) { ej = ( sj, aj, bj, s'j ) }, что длина теста совпадает с длиной подпоследовательности { ek(i) } и для каждого взаимодействия ( vi, xi, yi, v'i ) выполнены следующие условия:

пресостояние vi совпадает с
начальным состоянием целевой системы v0, если k(i) = 1;
ранее установленным состоянием ak(i)-1, если k(i) > 1 и ak (i)-1
V;
постсостоянием после предыдущей подачи стимула vi-1, если k(i) > 1 и ak(i)-1
X;
стимул xi совпадает с ak(i);
реакция yi совпадает с первым элементом реакции bk(i) = ( yk(i), vk(i) );
постсостояние v'i совпадает со вторым элементом реакции bk(i) = ( yk(i), vk(i) ).

Такой тест мы будем обозначать T( σ, v0 ).

Тестовый сценарий определяет последовательность тестовых действий, которая может варьироваться в зависимости от поведения целевой системы в процессе тестирования. Результатом работы тестового сценария является тест, состоящий из последовательности взаимодействий с целевой системой.

Далее, мы введем вспомогательное определение тестового сценария с внутренними переходами, которое будет использоваться для описания тестовых сценариев в более компактной форме.

Тестовым сценарием с внутренними переходами для целевой системы с интерфейсом ( X, Y, V ) называется пара ( C, s0 ), где

C - управляющий автомат ( S, A, B, E, Q ), в котором
множество стимулов A X
V
{ ε },
множество реакций B (Y x V)
{ ε },
множество переходов включает в себя только переходы ( s, a, b, s' ), в которых либо a
X и b
(Y x V), либо a
V
{ ε } и b = ε;
s0 : V
S - функция инициализации.

Основной особенностью данного определения является дополнительный элемент множества стимулов ε, который обозначает внутренний переход управляющего автомата.

Каждому тестовому сценарию с внутренними переходами σε = ( ( S, A, B, E, Q ), s0 ) соответствует тестовый сценарий σ( σε ) = ( ( S, A', B, E', Q' ), s0 ), в котором

множество стимулов A' = X
V,
множество переходов E' состоит из переходов ( s, a, b, s' )
S x A' x B x S, для которых существует путь s1
s2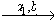
…
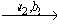sn в управляющем автомате ( S, A, B, E, Q ), удовлетворяющий следующим условиям: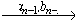
начальное состояние пути s1 = s,
конечное состояние пути sn = s',
i
{ 1, …, n-1 }: (ai = a)
(bi = b)

j
{ 1, …, n-1 } (i ≠ j)
(aj = ε)
(bj = ε);
множество заключительных состояний Q' состоит из состояний множества Q, а также из состояний s
S, из которых не выходит ни одного перехода во множестве E', но существует путь s1
s2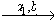
…
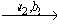sn в управляющем автомате ( S, A, B, E, Q ), в котором: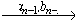
начальное состояние s1 = s,
конечное состояние sn
Q,
i
{ 1, …, n } (ai = ε)
(bi = ε).

Определение 5.

Механизмом построения тестового сценария называется функция, значением которой является тестовый сценарий.

Механизмы построения тестового сценария применяются для создания тестовых сценариев на основе каких-либо данных. Примером такого механизма может быть последовательная композиция набора тестовых сценариев.

В технологии UniTesK реализовано несколько механизмов построения тестового сценария. Наиболее важный из них - автоматный механизм построения тестового сценария, который является настолько гибким и удобным, что именно он используется для построения подавляющего большинства тестовых сценариев.

Содержание раздела